

Transitions and multistability in macroevolutionary dynamics of large mammals
SIMONA BEKERAITĖ, ROBERTAS STANKEVIČ, IVONA JUCHNEVIČIŪTĖ, KRISTIAN AGASØSTER HAAGA, and ANDREJ SPIRIDONOV
Bekeraitė, S., Stankevič, R., Juchnevičiūtė, I., Haaga, K.A., and Spiridonov, A. 2025. Transitions and multistability in macroevolutionary dynamics of large mammals. Acta Palaeontologica Polonica 70 (3): 479–494.
On multi-million-year timescales, the climate system of the Earth exhibits complex wandering behaviour. We investigate the evolutionary impacts of long-term climate change by analysing the dynamics of Cenozoic mammal evolution, looking for the presence of state transitions, stable equilibrium states and their association with long-term climate evolution. We perform Bayesian modelling of Artiodactyla, Carnivora, and Perissodactyla evolutionary histories. We then use recurrence plot analysis of the species richness time series, identifying the main transitions and regimes in large mammal evolution. Joint recurrence plots of diversity-Cenozoic oxygen isotope record as well as recurrence quantification analysis are used to further investigate the coupled dynamics of climate and mammal evolution. We find that several transitions between different states of the long-term climate evolution correspond to subsequent transitions and multistable states of diversity. The evidence for several climate transitions is recovered from joint recurrence states of diversity time series alone, indicating coordinated behaviour of three different mammalian orders and climate. The diversity fluctuations increase in amplitude during the Coolhouse regime in Oligocene and Miocene, with the diversity evolution starting an unprecedented decline during the Icehouse. Our results suggest that mammal diversity evolution has been coupled with the dynamical state of paleoclimate on multi-million-year timescales.
Key words: Mammalia, macroevolution, evolution, nonlinear dynamics, recurrence plots.
Simona Bekeraitė [simona.bekeraite@gmail.com; ORCID: https://orcid.org/0000-0001-5461-337X ], Robertas Stankevič [robertas.geo@gmail.com; ORCID: https://orcid.org/0009-0004-0280-3912 ], Ivona Juchnevičiūtė [ivona@juchneviciute.lt; ORCID: https://orcid.org/0009-0009-5610-6449 ], and Andrej Spiridonov [s.andrej@gmail.com, ORCID: https://orcid.org/0000-0002-8773-5629 ], Vilnius University, Department of Geology and Mineralogy, Faculty of Chemistry and Geosciences, M.K. Čiurlionio g. 21/27, Vilnius, 03101, Lithuania.
Kristian Agasøster Haaga [kahaaga@gmail.com; ORCID: https://orcid.org/0000-0001-6880-8725 ], University of Bergen, Department of Earth Science, Allégaten 41, Bergen, 5007, Norway; University of Bergen, Centre for Deep Sea Research, Allégaten 41, Bergen, 5007, Norway, Bjerknes Center for Climate Research, Jahnebakken 5, Bergen, 5007, Norway.
Received 21 February 2024, accepted 3 June 2025, published online 10 September 2025.
Copyright © 2025 S. Bekeraitė et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License (for details please see http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Introduction
Disentangling the impact of different drivers of evolution is a long-term objective of comprehensive macroevolutionary theory. The explanations for the forces driving the macroevolutionary change span the spectrum from the Red Queen Hypothesis emphasizing the impact of competition as the sole driver of evolution (Van Valen 1973) to the Court Jester Hypothesis (Barnosky 2001) which posits that environmental changes are the most relevant. Contemporary research concurs that there might be no single causal explanation of evolutionary change, instead offering a more nuanced, scale-dependent view of evolutionary responses to biotic and abiotic factors being intertwined, interacting at different, nested phylogenetic levels and temporal or spatial scales (Barnosky 2001; Benton 2009; Strotz et al. 2018; Novack-Gottshall and Lanier 2008; Spiridonov and Lovejoy 2023). At even longer timescales (comparable with the length of the Cenozoic), the biodiversity evolution is thought to enter the domain of the Geo-Red Queen and become self-stabilising due to tectonic process-led homogenisation (Spiridonov and Lovejoy 2022).
Recent research demonstrates that the Cenozoic climate evolution is a complex nonlinear process characterised by several tipping points leading to transitions between distinct climatic regimes (Westerhold et al. 2020; Marwan et al. 2021). During the last 66 Myr, the Earth’s climate system has passed through the so-called Warmhouse, Hothouse, Coolhouse, and Icehouse states characterised by differing degrees of chaotic behaviour, climatic variability and strength of response to astronomical forcing (Westerhold et al. 2020). On timescales larger than 1 Myr, climate evolution is characterised by a different scaling regime called megaclimate (Lovejoy 2015; Spiridonov and Lovejoy 2023) which exhibits unpredictable, wandering evolution throughout the Phanerozoic. Global climate transitions are predominantly driven by tectonic processes, subsequent changes in the global carbon cycle and nonlinear, state-dependent climate responses to astronomical forcing (Walker et al. 1981; Westerhold et al. 2020). Through the Cenozoic, the important geological processes include continent-reconfiguration driven changes in global ocean circulation patterns (Kennett 1977), Himalayan uplift and subsequent increase in weathering (Molnar et al. 1993), and the association between the North Atlantic Igneous Province and the Paleocene–Eocene Thermal Maximum (PETM) (Jones et al. 2019), among others.
Major shifts in climate are expected to induce species or higher-order taxa turnovers, the extent of which depends on the severity of the disturbance (Eldredge et al. 2003). The faunal response to the massive climatic changes throughout the Cenozoic is well documented (Blois and Hadly 2009), including adaptations such as hypsodonty increase in herbivores in response to cooling and drying climate (Jernvall and Fortelius 2002), or the connection between body size evolution and cooling pulses (Raia et al. 2012). Macroevolutionary processes can have systematically differing correlation patterns with climate fluctuations at different time scales (Barnosky 2001; Spiridonov and Lovejoy 2022).
Externally driven extinction events at the largest scales have a potential to reset the patterns of diversification (Van Valen 1984; Brayard et al. 2009; Alroy 2010). Therefore, time-dependent nonlinear responses of biodiversity can be expected in relation to climate forcing (Spiridonov et al. 2016). We propose interpreting the relationship between climate and diversity as an interaction between two coupled dynamical systems, one of which shows a long-scale wandering behaviour and the property of multistability, i.e., the presence of multiple stable equilibrium points. The transitions between different states of climate are then expected to induce subsequent transitions and states of diversity evolution. In this view, the biota responds to the climatic forcing in a systemic, self-organising manner, showing couplings between transitions and states instead of short-term responses to occasional random perturbations. Co-evolution of climate and biota can then be explored, describing the longest timescales of the Court Jester domain.
Despite multiple analyses which compare climate and diversity time series, or investigate faunal responses to distinct climatic events, a direct comparison of dynamical properties of climate evolution and mammalian diversity has, to our knowledge, not yet been performed. In this study, we present an analysis of the diversity dynamics of Artiodactyla, Carnivora, and Perissodactyla with a goal to reveal transitions between different states of diversity evolution regimes and to evaluate the degree of their synchronisation with the global climate transitions. We apply recurrence plot (RP) analysis and recurrence quantification analysis (RQA) to the time series, identifying nontrivial temporal patterns in the co-evolution of the Earth climate and mammalian diversity.
Recurrence plots are a nonlinear dynamics analysis and visualisation method first developed in statistical physics (Eckmann et al. 1995) and applied in many areas (Marwan et al. 2007), including palaeontology (Spiridonov et al. 2020; Rinkevičiūtė et al. 2022) and especially palaeoclimate research (Westerhold et al. 2020; Eroglu et al. 2016; Marwan et al. 2021). They can help identify periodic or non-periodic processes as well as transitions between different system states. For example, block-like structures in a recurrence plot show the presence of stable dynamical states of the system, such as the distinct climatic regimes in (Westerhold et al. 2020).
First, in the Material and methods section, we introduce the species richness data which we use to estimate the diversity trajectories through time, as well as the methods used, including a Bayesian reconstruction of Artiodactyla, Carnivora, and Perissodactyla evolutionary histories in Africa, Eurasia, and North America, and recurrence analysis. Then we describe the recovered evolutionary histories of Artiodactyla, Carnivora, and Perissodactyla and the results of recurrence analysis of the global climate and mammal diversity co-evolution patterns.
Abbreviations.—CEN, centrality of recurrence measure; EECO, Early Eocene Climatic Optimum; EOT, Eocene–Oligocene Transition; JRP, joint recurrence plot; mMCO, middle Miocene Climatic Optimum; mMCT, middle Miocene Climatic Transition; OMT, Oligocene–Miocene Transition; PETM, Paleocene/Eocene Thermal Maximum.
Material and methods
Paleodiversity and paleoenvironment datasets.—The NOW dataset, consisting of 68 350 records of fossil occurrences in 6166 localities (The NOW Community, retrieved 2022-04-27 from https://nowdatabase.org/; Žliobaitė et al. 2023), was pruned to include only well-defined species records of Eurasian, African, and North American Artiodactyla, Carnivora, and Perissodactyla, having minimum ages above 66 Myr and mean ages accurate to 20%. Several families of extant and extinct aquatic or semi-aquatic Carnivora (Enaliarctidae, Amphicynodontidae, Odobenidae, Otariidae, Phocidae) and predominantly South American Perissodactyla (Tapiridae) were excluded from the analysis.
For each occurrence of a species, its temporal range (minimum and maximum ages) was provided in the NOW database and used in further analysis. The final dataset consisted of 1670 Artiodactyla species (9081 occurrences), 1107 Carnivora species (5379 occurrences) and 738 Perissodactyla species (4766 occurrences). Species were classified into extant and extinct using the PanTHERIA database (Jones et al. 2009). There were 55 extant Artiodactyla species, 62 Carnivora, and 8 Perissodactyla species in our data, reflecting the incompleteness of the fossil record of even the extant species (Plotnick et al. 2016).
A detailed description of the sample, its comparison with the Paleobiology Database (PBDB, http://paleodb.org) and evaluation of the fossil record quality through time is provided in Appendix A. In particular, we identify two intervals (20–29 Myr and 38–48 Myr) in which the fossil record quality is reduced.
We used deep-sea benthic foraminifera isotope ratio (δ18O) record smoothed by a locally weighted function over a 1 Myr window, provided in the CENOGRID dataset (Westerhold et al. 2020) as proxy for global temperatures.
Diversification analysis.—Diversification analysis was performed using the PyRate v3.0 (Silvestro et al. 2014, 2019) Bayesian diversification analysis framework and its mcmcDivE method (Flannery-Sutherland et al. 2022). PyRate has a distinct advantage for our analysis of not binning the data into fixed age bins, which do not necessarily correspond to the biological processes under consideration. Instead, PyRate assigns a separate uncertainty range to each fossil occurrence and selects among models with different numbers of rate shifts, which allows recovering the most likely diversity (species richness) curves (Silvestro et al. 2019). Subsequent analysis using mcmcDivE yields corrected diversity curves by resampling the PyRate palaeodiversity estimates using temporal variations of preservation rates determined by the PyRate analysis.
In order to include the significant fossil age uncertainties in the NOW database, we followed the standard PyRate procedure of randomly sampling the occurrence ages from the uniform distributions defined by the maximum and minimum occurrence ages, repeating this procedure 20 times for each clade (Artiodactyla, Carnivora and Perissodactyla). PyRate analysis using the reversible jump MCMC algorithm implementation (RJMCMC) (Silvestro et al. 2019) was then performed on these 60 datasets after an exploratory analysis, which helped define the optimal model type, MCMC chain lengths and model parameters.
PyRate provides several possible approaches to modelling the preservation rates, describing different assumptions about the preservation rate variation, i.e., whether they are primarily expected to vary over the taxon lifetimes, over time, or between different lineages. The preservation rate model encompasses the outcomes of fossilization, discovery and classification processes, yielding the average expected number of fossils per species per million years. All three clades under consideration largely consist of large terrestrial mammals, albeit they have differing fossilisation likelihoods (Žliobaitė and Fortelius 2022). Assuming that the preservation rate heterogeneities in the three clades occur through geologic time, not among the species within a clade, we used the time-variable Poisson preservation rate model which assumes that the preservation rate within the clade is varying between predefined time windows and remains constant within them. We used a gamma prior on the preservation rates, using a fixed shape parameter (α = 1.5) and estimating the rate parameter β from the data during the modelling, using a vague hyperprior on β as described in (Silvestro et al. 2019).
The preservation rates were allowed to change at geological stage limits. Origination and extinction rate shifts were allowed to happen once in a million years (the default setting in PyRate).
The PyRate analysis was performed using Python 3.7 (available at http://www.python.org). We ran 10M iterations of MCMC sampling for Artiodactyla, Carnivora, and Perissodactyla. Every 10 000th sample was included. In further analysis, we rejected the initial 20% of each chain as burn-in, and resampled the chains again.
The MCMC analysis results were verified using the effective sample size estimates, diagnostic local efficiency and quantile efficiency plots (Vehtari et al. 2021), as well as visual inspection of autocorrelation lengths and trace plots using the Arviz package for Python (Kumar et al. 2019). We verified that the posterior ESS reached a value of at least 200. Generally, the model is quite complex especially given the large numbers of species in each clade, and the resulting large number of parameters. The most problematic (i.e., the slowest to converge) parameters are the discrete parameters describing the number of origination and extinction rate shifts (kbirth and kdeath), which is understandable given that the posterior distribution is forced to be multimodal by design, as the RJMCMC algorithm is jumping between different diversification models and provides the model-averaged results. We increased the relative frequency of reversible jump proposals from 0.1 to 0.2, using the -M 5 flag in PyRate.
Next we estimate corrected diversity trajectories by resampling them based on the estimated preservation rates through time and across lineages, using the mcmcDivE method (Flannery-Sutherland et al. 2022). We use 20 0000 MCMC iterations at 1 Myr intervals, then combining the multiple replicates for each clade and then calculating the diversity trajectories over time and their 95% confidence intervals. Absolute preservation rates (the average expected number of occurrences per species per Myr) estimated in the first part of the analysis are shown in Appendix A (Fig. A4).
Recurrence analysis.—A recurrence plot is a square, symmetric two-dimensional matrix of binary values which are defined to be equal to one (and shown in black in the graphical representation) at all moments in time when a trajectory is recurring, i.e., its value is close to a state in another time within a predetermined threshold (Marwan et al. 2007, 2021). The recurrence plot is thus populated by performing a pairwise comparison of all points in the time series.
Auto-recurrence plot analysis of the diversity time series was performed using the pyunicorn package for Python programming language (Donges et al. 2015). Following the analysis of Westerhold et al. 2020, we perform the recurrence analysis in time domain and set the recurrence threshold such that 10% of all points in the matrix were recurring. All time series values were normalised to (0, 1) before the analysis.
Joint recurrence plots (JRP) show the temporal structure of coordinated dynamics of systems evolving in different state spaces. The joint recurrence plot, a squared matrix
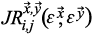
is described as the Hadamard product of two recurrence plot matrices:
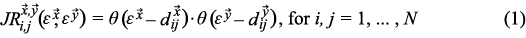
where θ (·) is the Heaviside step function, which assigns a value of one if the difference d is smaller or equal to the threshold value (ε), and zeroes otherwise;
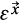
is the filtering threshold of the first recurrence plot and
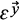
is the filtering threshold of the second recurrence plot, and
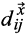
and
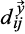
are distances of the two recurrence plots between the given time points i and j.
Joint recurrence plots were used to determine the joint dynamical behaviours in pairwise comparisons of Cenozoic oceanic foraminifera δ18O time series and the evolution of species richness of Artiodactyla, Carnivora, and Perissodactyla. In addition to the joint recurrence plots and analyses of pairs of variables, we constructed a joint recurrence plot of three species diversity time series of Artiodactyla, Carnivora, and Perissodactyla. This analysis was also performed using the pyunicorn package and the same ε value.
The triple joint recurrence plot
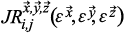
can be described in an analogous manner to Eq. 1 by adding a third variable z (Marwan et al. 2007):
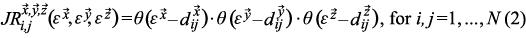
JRPs of all three clade diversity trajectories are used to test whether the coordination between climate and the biota can be detected without the input of any information from the climate proxy time series.
In order to characterise time-specific states detected in the recurrence and joint recurrence plots a recurrence quantification metric called the centrality of recurrence (CEN) was employed. It weights the recurrence rate (the ratio of recurring combinations and all combinations) against the dispersion of the recurrent states around the main diagonal (Spiridonov et al. 2017). The centrality of recurrence for a single column in a recurrence plot is mathematically defined as (Spiridonov et al. 2017):
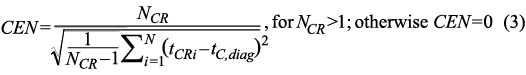
where CEN is the centrality of recurrence for a given column of the recurrence matrix, NCR is the number of the recurring combinations of times in the column, N is a number of rows (time bins) in a column, tCRi is the row number of the recurrent points in a column, and tC,diag is the row number of a diagonal point of the recurrence matrix in a given column.
CEN is optimised to detect dynamical states in recurrence plots which are consistently time-distinct, i.e., being unique in time and locally-autocorrelated in the case of recurrence plots and jointly time-unique and jointly locally autocorrelated for JRPs. In the context of the current work, CEN is used to measure the degree of time specificity of coordinated climate and species diversity dynamics of mammalian orders Artiodactyla, Carnivora, and Perissodactyla in joint recurrence plots.
CEN calculations were made using a custom code for the Perl programming language published in Spiridonov et al. (2017). CEN values were smoothed using a first-order Savitzky-Golay filter (Savitzky and Golay 1964) with a smoothing window of size s = 51.
Results
Evolutionary histories of Artiodactyla, Carnivora, and Perissodactyla.—In this work we used fossil occurrence data from the New and Old Worlds Database of Fossil Mammals (Žliobaitė et al. 2023; The NOW Community, retrieved 2022-04-27 from https://nowdatabase.org/). We present species richness histories (Fig. 1) and trajectories in species richness—δ18O space (Fig. 2) of Eurasian, African, and North American Artiodactyla, Carnivora, and Perissodactyla. The diversification analysis was performed using PyRate, a hierarchical Bayesian framework which simultaneously estimates fossil preservation, origination and extinction rates, as well as origination and extinction ages from fossil occurrence data, and its mcmcDivE method which provides diversity trajectories resampled according to the estimated preservation rates.
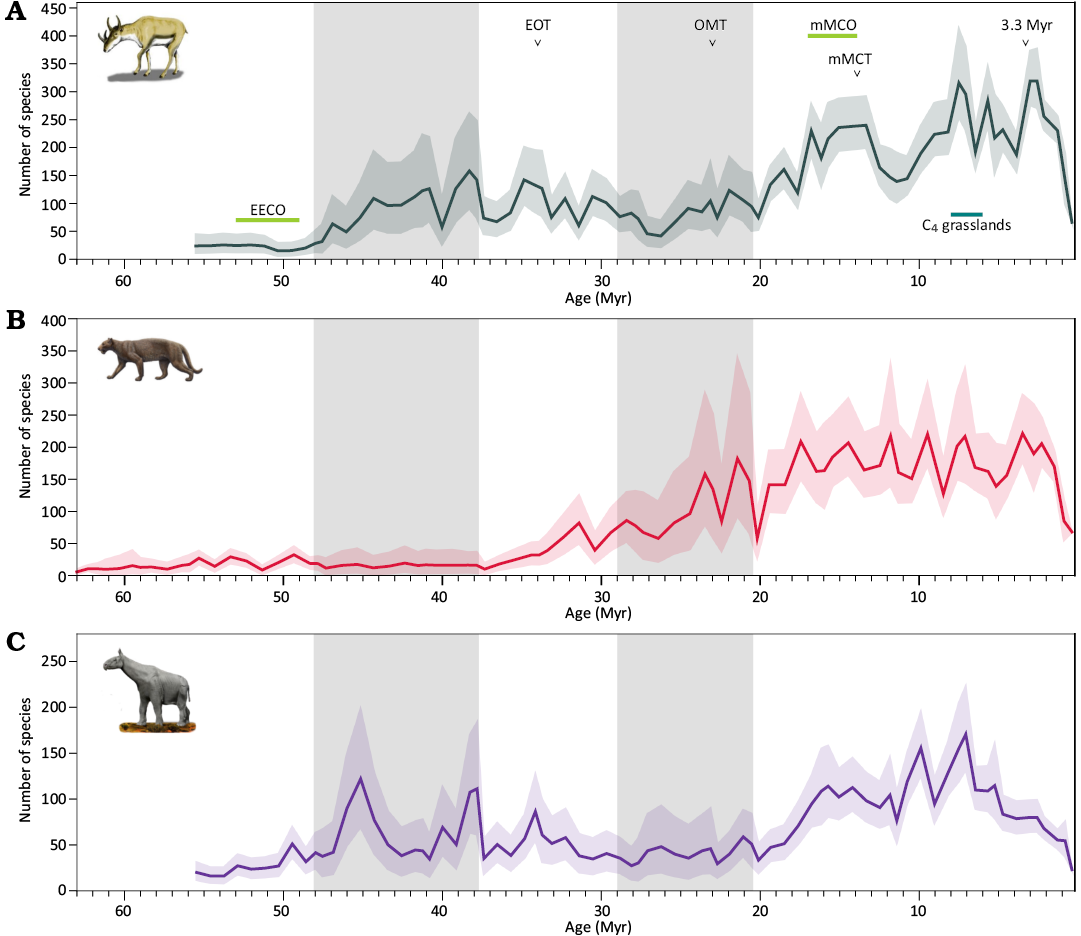
Fig. 1. Species richness histories of three large mammal clades: Artiodactyla (A), Carnivora (B), and Perissodactyla (C). Abbreviations: C4 grasslands, onset of C4 grassland spread between 8–6 Myr (Cerling et al. 1997; Strömberg 2011), 3.3 Myr, start of the Icehouse regime (mid-Pliocene Marine Isotope Stage M2); EECO, Early Eocene Climatic Optimum; EOT, Eocene–Oligocene Transition; mMCO, middle Miocene Climatic Optimum; mMCT, middle Miocene Climatic Transition; OMT, Oligocene–Miocene Transition; Grey shading marks two intervals of lower fossil record quality, as described in Appendix A. Syndyoceras cooki image by Nobu Tamura (Wikimedia Commons, CC-BY-SA 3.0). Paraceratherium sp. image by Tim Bertelink (Wikimedia Commons, CC-BY-SA 4.0). Dinictis felina illustration by Mauricio Anton (Wikimedia Commons, CC-BY-SA 3.0), published in Antón 2013.
Clade trajectories in the species richness—δ18O space, shown in Fig. 2, show similarities among the three clades and reveals an attractor-like behaviour of different climate regimes, as well as increasing variability of trajectories in both Coolhouse regimes. The apparent unravelling of diversity trajectory throughout the Icehouse illustrates the dramatic dynamic range of the Coolhouse-Icehouse climate transition and its impact on the mammal diversity. The δ18O values show a larger increase during the last 3.3 Myr than during the preceding 10 Myr after the middle Miocene Climatic Transition.
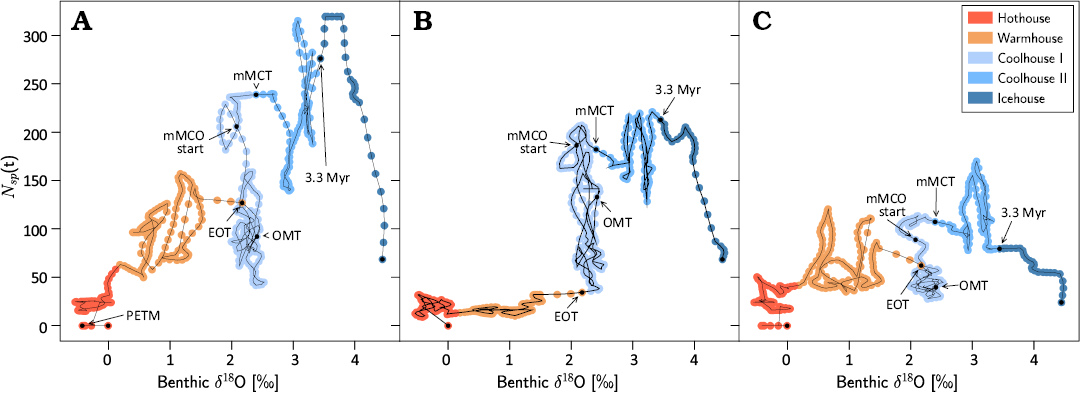
Fig. 2. Artiodactyla (A), Carnivora (B), and Perissodactyla (C) species richness Nsp(t) vs. deep-sea benthic foraminifera oxygen isotope record (Westerhold et al. 2020) values during the last 56.2 Myr. Points are colour-coded to reflect the temporal ranges of the Earth climate states (Warmhouse, Hothouse, the two distinct Coolhouse stages, and the Icehouse regime). Abbreviations: EOT, Eocene–Oligocene Transition; mMCO, onset of middle Miocene Climatic Optimum; mMCT, middle Miocene Climatic Transition; OMT, Oligocene–Miocene Transition; PETM, Paleocene/Eocene Thermal Maximum; 3.3 Myr, onset of the Icehouse regime 3.3 Myr ago (mid-Pliocene Marine Isotope Stage M2). The real extent of PETM δ18O excursion is not visible in the smoothed CENOGRID data. PETM δ18O values reached -2.5‰, as shown in Westerhold et al. 2020.
Recurrence analysis of species richness time series.—Recurrence analysis can be used to identify dynamical features such as persistent states, couplings between states, intermittency or state transitions of a nonlinear system even when direct time series analysis is not fruitful. Of a particular interest to palaeontology is the fact that recurrence plot analysis can be applied even when the assumption that the time series under consideration are much longer than the characteristic times of the system is not valid (Eckmann et al. 1995).
Following the methods used in the CENOGRID analysis (Westerhold et al. 2020), we use recurrence analysis of the species richness curves in order to recover the distinct dynamical states of Artiodactyla, Carnivora, and Perissodactyla diversity evolution. The species richness time series and their recurrence plots are presented in Fig. 3D2, displaying the recurrence plot of δ18O record from (Westerhold et al. 2020), analogous to panel B in their fig. 2, but with the temporal resolution downgraded to 2000 data points in order to enable a more reasonable comparison with the diversity time series.

Fig. 3. Recurrence plots of the mammal order species richness [Nsp(t)] and deep-sea benthic foraminifer oxygen isotope ratio record (δ18O) (Westerhold et al. 2020) time series. Artiodactyla (A1), Carnivora (B1), and Perissodactyla (C1) species richness. Deep-sea benthic foraminifer oxygen isotope ratio δ18O (D1). Recurrence plots of the four time series (A2–D2). Coloured ranges at the top of recurrence plots indicate the Earth climate states (Hothouse, Warmhouse, two Coldhouse states and Icehouse) (Westerhold et al. 2020). Grey shading marks two intervals of lower fossil record quality, as described in Appendix A. Abbreviations: C4 grasslands, onset of C4 grassland spread between 8–6 Myr; 3.3 Myr, onset of the Icehouse regime 3.3 Myr ago (mid-Pliocene Marine Isotope Stage M2); EECO, Early Eocene Climatic Optimum; EOT, Eocene–Oligocene Transition; mMCO, middle Miocene Climatic Optimum; mMCT, middle Miocene Climatic Transition; OMT, Oligocene–Miocene Transition; PETM, Paleocene–Eocene Thermal Maximum; Silhouettes of Haploidoceros mediterraneus, Smilodon fatalis, and Paraceratherium sp. obtained from http://phylopic. org/, CC BY-SA 3.0 and CC0 1.0 Universal Creative Commons licences. The time series data shown in panels (A1, B1, C1, etc.) have been rescaled to a range between 0 and 1.
We identify a number of distinct diversity states and transitions visible as separate blocks and their limits in our plots, to a large degree corresponding to previously identified transitions between fundamental climate regimes of the Earth (Westerhold et al. 2020) and illustrating different responses to climatic forcing exhibited by the three mammal orders.
A distinct regime during the hothouse phase of the Earth climate, between the Paleocene–Eocene Thermal Maximum (PETM) 56 Myr ago and the end of Early Eocene Climatic Optimum (EECO, ~47 Myr ago) is visible in the recurrence plots. Eocene–Oligocene Transition at ~34 Myr is evident in Carnivora and Perissodactyla recurrence plots, whereas slow and steady Artiodactyla diversification between EECO and Oligocene–Miocene Transition (OMT, ~23 Myr ago) was only briefly interrupted at around the Eocene–Oligocene Transition.
Both herbivore clades tentatively exhibit a state change at the Oligocene–Miocene Transition, however, this interval is not reliably represented in the fossil record, as described in Appendix A and the result should be treated with caution. A subsequent transition in the dynamics of all three clades is visible at around the onset of the Miocene Climatic Optimum, corresponding to significant diversity increase at the time.
Interpretation of the Perissodactyla recurrence plot is somewhat confounded by the multimodal shape of their diversity curve, i.e., the decline in diversity after the EOT, subsequent recovery during the first half of the Miocene and a sharp decline starting about 8 Myr ago. Recurrence between very different periods of time, separated by time intervals much longer than the lifetimes of species do not necessarily represent similar ecosystems and instead show similarities in the general species richness trajectory of the clade. These transitions are recovered in joint recurrence analysis in the following section.
The species richness record is affected by the decreasing quality of the fossil record with geological time, the effects of which cannot be fully rectified by accounting for the preservation rate in our model. As the number of recovered taxa decreases with time due to both poor fossil record and low diversification levels at the early stages of evolution of the clades, the Paleocene and Eocene time series are flatter and thus more self-similar, leading to less-detailed dark blocks representing the earlier states of diversity. The blocks representing diversity recurrence since the start of the Miocene exhibit less coarse structure. However, in this analysis we are looking for large-scale transitions between gross diversity states, with the shorter-period fluctuations being less pertinent.
Joint recurrence analysis of diversity evolution dynamics.—Joint recurrence plots (JRP) (Marwan et al. 2007) are a multivariate extension of recurrence plots, comparing the joint recurrence behaviour of two or more different dynamical systems. It allows detecting and analysing the synchronisation types and extent between the systems irrespectively of the causal mechanisms in action.
JRP of climate and diversity time series are presented in Fig. 4. Distinct states of joint recurrence are discernible in the plots, to a large degree corresponding to the gross Cenozoic climatic states, but showing a somewhat different view for evolution after the Eocene–Oligocene Transition. Perissodactyla demonstrates the largest number of distinct transitions and dynamical states, followed by Artiodactyla. Clade diversity—δ18O joint recurrence plots implicate the presence of not two, but three or four distinct states of diversity-climate dynamics during the Coolhouse regime. The onset of the Miocene Climatic Optimum, shown in the previous chapter to be a point of an important diversity regime transition, here is demonstrated to be a beginning of a separate state of climate-diversity evolution.
Remarkably, even the joint recurrence plot of the three diversity time series (Fig. 4D) shows the transitions at EOT, OMT, and the onset of the MCO, and the distinct regimes between the transitions without using any information from the δ18O time series. This indicates that important climatic transitions and regimes are imprinted in the diversity patterns of the three separate orders, affecting their diversity trajectories for millions of years, and points towards correlated behaviour of the climate system and mammalian diversity.
Figure 4 also shows the smoothed centrality of recurrence (CEN) measure (Spiridonov et al. 2017), also described in the Materials and methods section. A direct comparison between all four CEN curves and their discussion can be found in Appendix B.
The CEN time series is a running measure of the time-uniqueness of a state at specific times and illustrates the common features of mammalian diversity and paleotemperature time series and the inter-clade diversity times series ( Fig. 4D 3). Miocene and Pliocene epochs corresponded to the highest species richness levels in the studied clades, simultaneously exhibiting much higher variability of diversity dynamics in all clades than in the other epochs. Systematically higher values of recurrence centrality during the Paleogene and Quaternary show that the joint dynamics of the climate and species diversity during the Paleogene and especially during the Quaternary were more time-specific and also more autocorrelated than during the Neogene.
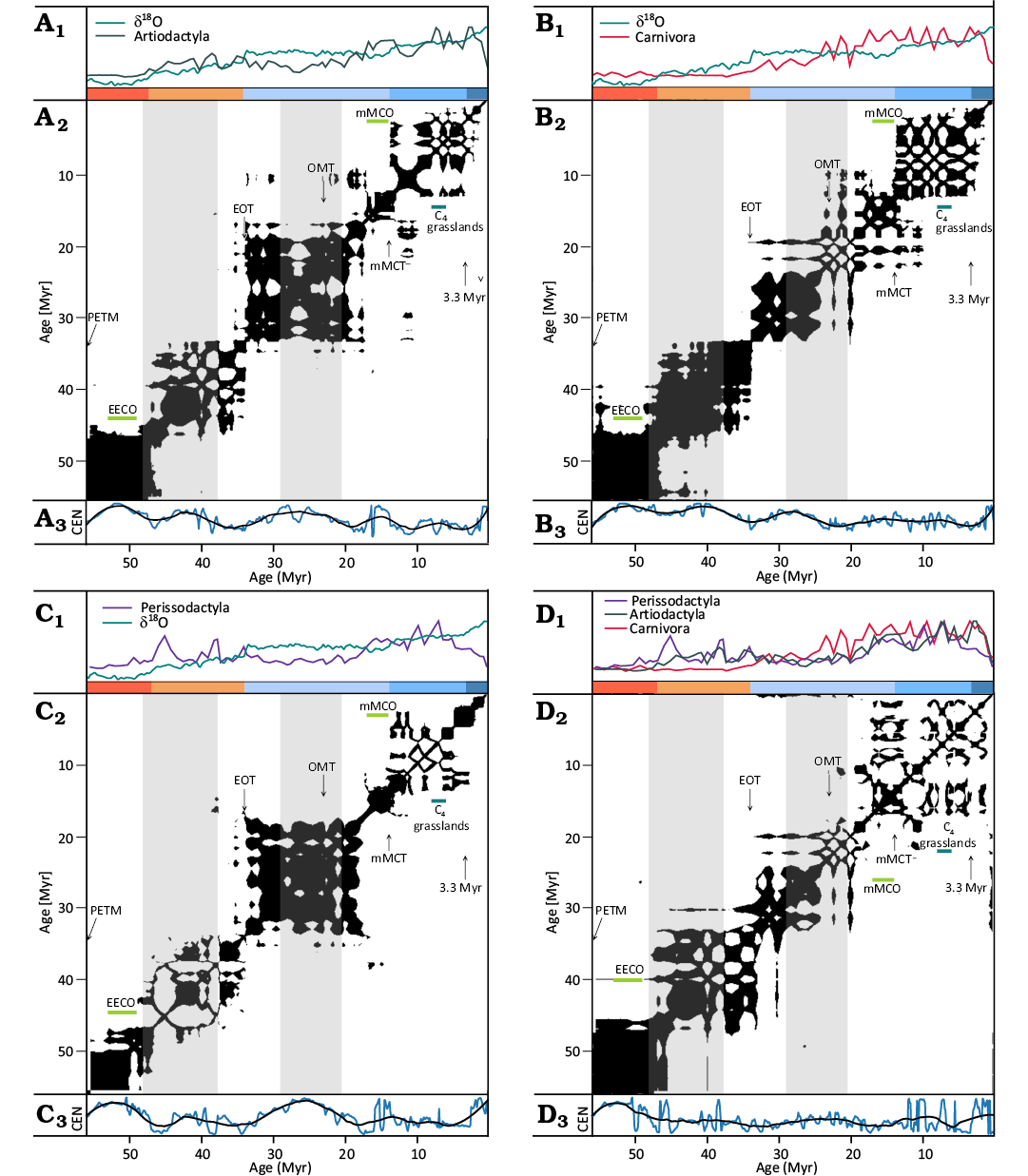
Fig. 4. Joint recurrence plots (A1–D1); joint recurrence plots of the four combinations of the time series between 56.2–0.2 Myr. (A2–D2); centrality of recurrence (CEN) measure over time, as described in the text (A3–D3) for Artiodactyla (A), Carnivora (B), and Perissodactyla (C) diversity and δ18O. D. All three mammalian diversity time series. Coloured ranges at the top of the recurrence plots mark the Earth climate states (Westerhold et al. 2020). Grey shading marks two intervals of lower fossil record quality, as described in Appendix A. Abbreviations: C4 grasslands, onset of C4 grassland spread, 3.3 Myr: onset of the Icehouse regime 3.3 Myr ago; EECO, Early Eocene Climatic Optimum; EOT, Eocene–Oligocene Transition; mMCO, middle Miocene Climatic Optimum; mMCT, middle Miocene Climatic Transition; OMT, Oligocene–Miocene Transition; 3.3 Myr, onset of the Icehouse regime.. The time series data shown in panels (A1, B1, C1, etc.) have been rescaled to a range between 0 and 1
Discussion
Our findings suggest that the mammalian species richness evolution has been coupled with paleoclimate states on multi-million-year timescales, showing regime transitions and persistent states related to those recovered in the Cenozoic oxygen isotope record. We find that the diversity fluctuations increase in amplitude during the Coolhouse climate in Oligocene and Miocene–Pleistocene, demonstrating a clade-dependent number of dynamical substates. During the Icehouse climatic regime which started 3.3 Myr ago, mammalian diversity entered a long-term state of decline corresponding to increasingly harsh climatic conditions. The imprint of three Cenozoic climatic events (Eocene–Oligocene and Oligocene–Miocene transitions the onset of Miocene Climatic Optimum) is discernible even when only the joint diversity recurrence of the three clades is considered, indicating the presence of climate-driven faunal diversity transitions on the global scale.
Recurrence analysis enables recovering the correlations present in the behaviour of the climate and diversity evolution.
We demonstrate that different climate regimes act as attractors of diversity evolution, modulating the diversification and expansion of Cenozoic mammals that started in the Paleocene. The diversity trajectories become more unstable after the Eocene–Oligocene Transition and especially after the middle Miocene Climatic Transition, likely as the result of increased sensitivity of the Earth system to astronomical perturbations in the Coolhouse state (Westerhold et al. 2020). Joint recurrence analysis indicates the presence of several distinct regimes of diversity-climate dynamics during the Oligocene and Miocene, with the herbivore lineages showing a higher number of states.
A connection between the global temperature, family and genus diversity as well as the origination and extinction rates, was reported in Mayhew et al. (2008). The authors state that de-trended global diversity during the last 520 Myr was negatively correlated with de-trended temperature and showed high origination and extinction rates during the greenhouse climate phases. Our analysis shows a persistent mammal diversity increase with the cooling climate of the Cenozoic, however, mammal diversity drops in the late Cenozoic indicating that at least for large land mammals the relationship between diversity and global temperature is not linear.
Large-scale mammal species richness evolution patterns throughout the Cenozoic are a product of multiple environmental processes, the impacts of which are not easy to disentangle. Climate-driven adaptation to new niches, continent fragmentation and isolated diversification of specialist taxa (Janis 1993; Gheerbrant and Rage 2006), sea-level drop- or tectonic uplift-driven land bridge formation and subsequent faunal exchanges, as well as diversity reduction attributed to the increasingly harsh climate during the previous few millions of years are among the possible mechanisms of climate influence on diversity. At the species level, climatic shifts cause habitat fragmentation, leading to isolation of populations and adaptive speciation as described by the turnover pulse hypothesis (Vrba 1992, 1993). We offer a complementary interpretation of the lock-step transitions of diversity: in addition to generating pulses of evolutionary turnover, quasi-discrete transitions in climate determine the new carrying capacities of the ecosystems in which the large mammals live. As an example, the fraction of primary productivity available to larger animals tends to increase in cooler and more seasonal climatic conditions, also leading to secondary effects on the carnivorous clades (Oksanen 2019).
We confirm the prediction that on the multi-million-year timescales, the diversity transitions and transient multistable states are correlated with the laminar states of the megaclimate. Our findings confirm the predictions of the multilevel mixed model of evolution (Benton 2009) and reaffirm the view that on very long timescales, evolution is controlled by the physical environment (Eldredge et al. 2003). Our results complement the classical picture of macroevolutionary response to environmental change (Alroy 2010). In the latter, a strong but transient environmental perturbation is expected to reset the carrying capacities and diversification rates at high taxonomic levels, which remain independent from the background trends. In our view, climate transitions reset the diversity dynamics by sending diversity trajectories on their way to another attractor. A conceptual illustration of the difference between the two paradigms is provided in Appendix C. Significant transitions between diversity regimes are expected in both cases, however, in our view, the multistable diversity equilibria are not autonomous states independent from the driving climate. Instead, diversity evolution is directly coupled with the dynamic state of the underlying megaclimate.
The relatively recent high biodiversity state might be considered to be a transient phenomenon, brought about by a high degree of continental fragmentation after the breakup of Pangea (Spiridonov and Lovejoy 2022) and subsequent parallel evolution of placental mammals on different continents. Analysis of evolutionary dynamics of lineages older than Mammalia could shed light on this assumption.
Another potential avenue for future research is explicitly modelling the diversification processes and the resulting data properties, applying causal inference methods and thus testing the limits of detectability of causal relations in such data. This finding does not negate the correlated behaviour of climate and diversity detected in the recurrence plots. Instead, our results demonstrate the potential of nonlinear time series analysis (Marwan et al. 2021) and the need for rigorous statistical analyses in palaeontology.
Acknowledgements
We sincerely thank the editor and the reviewers for their attentive reading of and constructive feedback on the previous versions of this manuscript. We believe it has been significantly improved as a result. SB thanks Daniele Silvestro (Eidgenössische Technische Hochschule Zürich, Switzerland) and Indrė Žliobaitė (University of Helsinki, Finland) for useful advice and support, and Gerda Vaitkevičiūtė (Vilnius, Lithuania) for technical assistance. We also are grateful for HPC resources provided by the IT Research Center of Vilnius University. SB was supported by the Research Council of Lithuania grant 09.3.3-LMT-K-712-19-0129, “Multivariate evolutionary response of terrestrial fauna to biotic and abiotic factors during Cenozoic: probabilistic determination of causal relations”.
Editor: Eli Amson
References
Alroy, J. 2008. Dynamics of origination and extinction in the marine fossil record. Proceedings of the National Academy of Sciences 105: 11536–11542. Crossref
Alroy, J. 2010. The shifting balance of diversity among major marine animal groups. Science 329: 1191–1194. Crossref
Antell, G.T., Benson, R.B., and Saupe, E.E. 2023. Spatial standardization of taxon occurrence data—a call to action. Paleobiology 50 (2): 1–17. Crossref
Antón, M. 2013. Walking with sabertooths: Using science and art to shed light on the ultimate predators. Cranium 30: 36–43.
Barnosky, A.D. 2001. Distinguishing the effects of the Red Queen and Court Jester on Miocene mammal evolution in the northern Rocky Mountains. Journal of Vertebrate Paleontology 21: 172–185. Crossref
Benton, M.J. 2009. The Red Queen and the Court Jester: species diversity and the role of biotic and abiotic factors through time. Science 323: 728–732. Crossref
Benton, M.J., Dunhill, A.M., Lloyd, G.T., and Marx, F.G. 2011. Assessing the quality of the fossil record: insights from vertebrates. Geological Society, London, Special Publications 358: 63–94. Crossref
Benton, M.J., Wills, M., and Hitchin, R. 2000. Quality of the fossil record through time. Nature 403: 534–537. Crossref
Blois, J.L. and Hadly, E.A. 2009. Mammalian response to Cenozoic climatic change. Annual Review of Earth and Planetary Sciences 37: 181–208. Crossref
Brayard, A., Escarguel, G., Bucher, H., Monnet, C., Brühwiler, T., Goudemand, N., Galfetti, T., and Guex, J. 2009. Good genes and good luck: ammonoid diversity and the end-Permian mass extinction. Science 325: 1118–1121.
Brett, C.E. and Baird, G.C. 1997. Epiboles, outages, and ecological evolutionary bioevents: Taphonomic, ecological, and biogeographic factors. In: C.E. Brett and G.C. Baird (eds.), Paleontological Events, 249–284. Columbia University Press, New York.
Cantalapiedra, J.L., Hernandez Fernandez, M., Azanza, B., and Morales, J. 2015. Congruent phylogenetic and fossil signatures of mammalian diversification dynamics driven by Tertiary abiotic change. Evolution 69: 2941–2953. Crossref
Cerling, T.E., Harris, J.M., MacFadden, B.J., Leakey, M.G., Quade, J., Eisenmann, V., and Ehleringer, J.R. 1997. Global vegetation change through the Miocene/Pliocene boundary. Nature 389: 153–158. Crossref
Clyde, W.C. 1997. Stratigraphy and Mammalian Paleontology of the McCullough Peaks, Northern Bighorn Basin, Wyoming: Implications for Biochronology, Basin Development, and Community Reorganization across the Paleocene–Eocene Boundary. 271 pp. Doctoral Dissertation, University of Michigan, Ann Arbor.
Crampton, J.S., Cooper, R.A., and Sadler, P.M., Foote, M. 2016. Greenhouse—icehouse transition in the Late Ordovician marks a step change in extinction regime in the marine plankton. Proceedings of the National Academy of Sciences 113: 1498–1503. Crossref
Crampton, J.S., Meyers, S.R., Cooper, R.A., Sadler, P.M., Foote, M., and Harte, D. 2018. Pacing of Paleozoic macroevolutionary rates by Milankovitch grand cycles. Proceedings of the National Academy of Sciences 115: 5686–5691. Crossref
Donges, J.F., Heitzig,
J., Beronov, B., Wiedermann, M., Runge, J., Feng, Q.Y., Tupikina, L.,
Stolbova, V., Donner, R.V., Marwan, N., Dijkstra, H.A., and Kurths, J.
2015. Unified functional network and nonlinear time series analysis
for complex systems science: The pyunicorn
package. Chaos: An Interdisciplinary
Journal of Nonlinear Science 25: 113101. Crossref
Eckmann, J.P., Kamphorst, S.O., and Ruelle, D. 1995. Recurrence plots of dynamical systems. World Scientific Series on Nonlinear Science, Series A 16: 441–446. Crossref
Eldredge, N., Crutchfield, J.P., and Schuster, P. 2003. The sloshing bucket: how the physical realm controls evolution. In: J.P. Crutchfield and P. Schuster (eds.), Evolutionary Dynamics: Exploring the Interplay of Selection, Accident, Neutrality, and Function (SFI Studies in the Sciences of Complexity Series), 3–32. Oxford University Press, New York.
Eroglu, D., McRobie, F.H., Ozken, I., Stemler, T., Wyrwoll, K.H., Breitenbach, S.F., Marwan, N., and Kurths, J. 2016. See-saw relationship of the Holocene East Asian–Australian summer monsoon. Nature Communications 7: 12929. Crossref
Flannery-Sutherland, J.T., Silvestro, D., and Benton, M.J. 2022. Global diversity dynamics in the fossil record are regionally heterogeneous. Nature Communications 13: 2751. Crossref
Fortelius, M., Agustí, J., Bernor, R.L., de Bruijn, H., van Dam, J.A., Damuth, J., Eronen, J. T., Evans, G., van den Hoek Ostende, L.W., Janis, C.M., Jernvall, J., Kaakinen, A., von Koenigswald, W., Lintulaakso, K., Liu, L., Ataabadi, M.M., Mittmann, H., Pushkina, D., Saarinen, J., Sen, S., Sova, S., Säilä, L.K., Tesakov, A., Vepsäläinen, J., Viranta, S., Vislobokova, I., Werdelin, L., Zhang, Z., and Žliobaitė, I. 2023. The origin and early history of now as it happened. In: I. Casanovas-Vilar, L.W. van den Hoek Ostende, C.M. Janis, and J. Saarinen (eds.), Evolution of Cenozoic Land Mammal Faunas and Ecosystems: 25 Years of the NOW Database of Fossil Mammals, 7–32. Springer, Cham Crossref
Gheerbrant, E. and Rage, J.C. 2006. Paleobiogeography of Africa: how distinct from Gondwana and Laurasia? Palaeogeography, Palaeoclimatology, Palaeoecology 241: 224–246. Crossref
Good, I.J. 1953. The population frequencies of species and the estimation of population parameters. Biometrika 40: 237–264. Crossref
Janis, C. 1993. Tertiary mammal evolution in the context of changing climates, vegetation, and tectonic events. Annual Review of Ecology and Systematics 24: 467–500. Crossref
Jeppsson, L. 1987. Lithological and conodont distributional evidence for episodes of anomalous oceanic conditions during the Silurian. In: R. Aldridge (ed.), Palaeobiology of Conodonts, 129–145. Ellis Horwood Ltd, Chichester.
Jernvall, J. and Fortelius, M. 2002. Common mammals drive the evolutionary increase of hypsodonty in the Neogene. Nature 417: 538–540. Crossref
Jones, K.E., Bielby, J., Cardillo, M., Fritz, S.A., O’Dell, J., Orme, C.D.L., Safi, K., Sechrest, W., Boakes, E.H., Carbone, C., and Connoly, C. 2009. Pantheria: a species-level database of life history, ecology, and geography of extant and recently extinct mammals: Ecological Archives E090-184. Ecology 90: 2648–2648. Crossref
Jones, S.M., Hoggett, M., Greene, S.E., and Dunkley Jones, T. 2019. Large Igneous Province thermogenic greenhouse gas flux could have initiated Paleocene–Eocene Thermal Maximum climate change. Nature Communications 10: 5547. Crossref
Kennett, J.P. 1977. Cenozoic evolution of Antarctic glaciation, the circum-Antarctic Ocean, and their impact on global paleoceanography. Journal of Geophysical Research 82: 3843–3860. Crossref
Kocsis, Á.T., Reddin, C.J., Alroy, J., and Kiessling, W. 2019. The R package DivDyn for quantifying diversity dynamics using fossil sampling data. Methods in Ecology and Evolution 10: 735–743. Crossref
Kumar, R., Carroll, C., Hartikainen, A., and Martin, O. 2019. ArviZ: a unified library for exploratory analysis of Bayesian models in Python. Journal of Open Source Software 4: 1143. Crossref
Liow, L.H. and Finarelli, J.A. 2014. A dynamic global equilibrium in carnivoran diversification over 20 million years. Proceedings of the Royal Society B: Biological Sciences 281: 20132312. Crossref
Liow, L.H., Fortelius, M., Bingham, E., Lintulaakso, K., Mannila, H., Flynn, L., and Stenseth, N.C. 2008. Higher origination and extinction rates in larger mammals. Proceedings of the National Academy of Sciences 105: 6097–6102. Crossref
Lourens, L.J. 2008. On the Neogene–Quaternary debate. Episodes Journal of International Geoscience 31: 239–242. Crossref
Lovejoy, S. 2015. A voyage through scales, a missing quadrillion and why the climate is not what you expect. Climate Dynamics 44: 3187–3210. Crossref
Mannion, P.D. and Upchurch, P. 2010. Completeness metrics and the quality of the sauropodomorph fossil record through geological and historical time. Paleobiology 36: 283–302. Crossref
Marwan, N., Donges, J.F., Donner, R.V., and Eroglu, D. 2021. Nonlinear time series analysis of palaeoclimate proxy records. Quaternary Science Reviews 274: 107245. Crossref
Marwan, N., Romano, M.C., Thiel, M., and Kurths, J. 2007. Recurrence plots for the analysis of complex systems. Physics Reports 438: 237–329. Crossref
Mayhew, P.J., Jenkins, G.B., and Benton, T.G. 2008. A long-term association between global temperature and biodiversity, origination and extinction in the fossil record. Proceedings of the Royal Society B: Biological Sciences 275: 47–53. Crossref
Molnar, P., England, P., and Martinod, J. 1993. Mantle dynamics, uplift of the Tibetan Plateau, and the Indian monsoon. Reviews of Geophysics 31: 357–396. Crossref
New and Old Worlds Database of Fossil Mammals (NOW). The NOW Community, retrieved 2022-04-27 from https://nowdatabase.org/.
Novack-Gottshall, P.M. and Lanier, M.A. 2008. Scale-dependence of Cope’s rule in body size evolution of Paleozoic brachiopods. Proceedings of the National Academy of Sciences 105: 5430–5434. Crossref
Oksanen, O. 2019. Patterns of relative abundance among large Carnivora in western Eurasia during the Plio-Pleistocene. Evolutionary Ecology Research 20: 615–638.
Peters, S.E. and Heim, N.A. 2010. The geological completeness of paleontological sampling in North America. Paleobiology 36: 61–79. Crossref
Plotnick, R.E., Smith, F.A., and Lyons, S.K. 2016. The fossil record of the sixth extinction. Ecology Letters 19: 546–553. Crossref
Prothero, D. 2015. Garbage in, garbage out: the effects of immature taxonomy on database compilations of North American fossil mammals. New Mexico Museum of Natural History and Science Bulletin 68: 257–264.
Raia, P., Carotenuto, F., Passaro, F., Fulgione, D., and Fortelius, M. 2012. Ecological specialization in fossil mammals explains Cope’s rule. The American Naturalist 179: 328–337. Crossref
Rinkevičiūtė, S., Stankevič, R., Radzevičius, S., Meidla, T., Garbaras, A., and Spiridonov, A. 2022. Dynamics of ostracod communities throughout the Mulde/lundgreni event: contrasting patterns of species richness and palaeocommunity compositional change. Journal of the Geological Society 179: jgs2021–039. Crossref
Savitzky, A. and Golay, M.J. 1964. Smoothing and differentiation of data by simplified least squares procedures. Analytical Chemistry 36: 1627–1639. Crossref
Silvestro, D., Salamin, N., Antonelli, A., and Meyer, X. 2019. Improved estimation of macroevolutionary rates from fossil data using a Bayesian framework. Paleobiology 45: 546–570. Crossref
Silvestro, D., Schnitzler, J., Liow, L.H., Antonelli, A., and Salamin, N. 2014. Bayesian estimation of speciation and extinction from incomplete fossil occurrence data. Systematic Biology 63: 349–367. Crossref
Spiridonov, A., Brazauskas, A., and Radzevičius, S. 2016. Dynamics of abundance of the mid-to-late Pridoli conodonts from the Eastern part of the Silurian Baltic Basin: multifractals, state shifts, and oscillations. American Journal of Science 316: 363–400. Crossref
Spiridonov, A. and Lovejoy, S. 2022. Life rather than climate influences diversity at scales greater than 40 million years. Nature 607: 307–312. Crossref
Spiridonov, A. and Lovejoy, S. 2023. Scaling in the evolution of biodiversity. Biological Theory 18 (1): 1–6. Crossref
Spiridonov, A., Stankevič, R., Gečas, T., Brazauskas, A., Kaminskas, D., Musteikis, P., Kaveckas, T., Meidla, T., Bičkauskas, G., Ainsaar, L., and Radzevičius, S. 2020. Ultra-high resolution multivariate record and multiscale causal analysis of Pridoli (late Silurian): implications for global stratigraphy, turnover events, and climate-biota interactions. Gondwana Research 86: 222–249. Crossref
Spiridonov, A., Stankevič, R., Gečas, T., Šilinskas, T., Brazauskas, A., Meidla, T., Ainsaar, L., Musteikis, P., and Radzevičius, S. 2017. Integrated record of Ludlow (Upper Silurian) oceanic geobioevents-coordination of changes in conodont, and brachiopod faunas, and stable isotopes. Gondwana Research 51: 272–288. Crossref
Strömberg, C.A. 2011. Evolution of grasses and grassland ecosystems. Annual Review of Earth and Planetary Sciences 39: 517–544. Crossref
Strotz, L.C., Simoes, M., Girard, M.G., Breitkreuz, L., Kimmig, J., and Lieberman, B.S. 2018. Getting somewhere with the Red Queen: chasing a biologically modern definition of the hypothesis. Biology Letters 14: 20170734. Crossref
Van Dam, J.A., Abdul Aziz, H., Angeles Alvarez Sierra, M., Hilgen, F.J., van den Hoek Ostende, L.W., Lourens, L.J., Mein, P., van Der Meulen, A.J., and Pelaez-Campomanes, P. 2006. Long-period astronomical forcing of mammal turnover. Nature 443: 687–691. Crossref
Van Valen, L.M. 1973. A new evolutionary law. Evolutionary Theory 1: 1–30.
Van Valen, L.M. 1984. A resetting of Phanerozoic community evolution. Nature 307: 50–52. Crossref
Vehtari, A., Gelman, A., Simpson, D., Carpenter, B., and Bürkner, P.C. 2021. Rank-normalization, folding, and localization: An improved R for assessing convergence of MCMC. Bayesian Analysis 16: 667–718. Crossref
Vrba, E.S. 1992. Mammals as a key to evolutionary theory. Journal of Mammalogy 73: 1–28. Crossref
Vrba, E.S. 1993. Turnover-pulses, the Red Queen, and related topics. American Journal of Science 293: 418. Crossref
Walker, J.C., Hays, P., and Kasting, J.F. 1981. A negative feedback mechanism for the long-term stabilization of Earth’s surface temperature. Journal of Geophysical Research: Oceans 86: 9776–9782. Crossref
Westerhold, T., Marwan, N., Drury, A.J., Liebrand, D., Agnini, C., Anagnostou, E., Barnet, J.S.K., Bohaty, S.M., De Vleeschouwer, D., Florindo, F., Frederichs, T., Hodell, D.A., Holbourn, A.E., Kroon, D., Lauretano, V., Littler, K., Lourens, L.J., Lyle, M., Pälike, H., Röhl, U., Tian, J., Wilkens, R.H., Wilson, P.A., and Zachos, J.C. 2020. An astronomically dated record of Earth’s climate and its predictability over the last 66 million years. Science 369: 1383–1387. Crossref
Žliobaitė, I. and Fortelius, M. 2022. On calibrating the completometer for the mammalian fossil record. Paleobiology 48: 1–11. Crossref
Žliobaitė, I., Fortelius, M., Bernor, R.L., van den Hoek Ostende, L.W., Janis, C.M., Lintulaakso, K., Säilä, L.K., Werdelin, L., Casanovas-Vilar, I., Croft, D.A., Flynn, L.J., Hopkins, S.S.B., Kaakinen, A., Kordos, L., Kostopoulos, D.S., Pandolfi, L., Rowan, J., Tesakov, A., Vislobokova, I., Zhang, Z., Aiglstorfer, M., Alba, D.M., Arnal, M., Antoine, P.O., Belmaker, M., Bilgin, M., Boisserie, J.R., Borths, M.R., Cooke, S.B., van Dam, J.A., Delson, E., Eronen, J.T., Fox, D., Friscia, A.R., Furió, M., Giaourtsakis, I.X., Holbrook, L., Hunter, J., López-Torres, S., Ludtke, J., Minwer-Barakat, R., van der Made, J., Mennecart, B., Pushkina, D., Rook, L., Saarinen, J., Samuels, J.X., Sanders, W., Silcox, M.T., Vepsäläinen, J. 2023. The NOW database of fossil mammals. In: I. Casanovas-Vilar, L.W. van den Hoek Ostende, C.M. Janis, and J. Saarinen (eds.),, Evolution of Cenozoic Land Mammal Faunas and Ecosystems: 25 Years of the NOW Database of Fossil Mammals, 33–42. Springer, Cham. Crossref
Characterisation of the Artiodactyla, Carnivora, and Perissodactyla fossil record
In this section we describe the rationale of our sample selection, its geographic and temporal characterisation and estimates of its quality through the Cenozoic.
As described in the Material and methods section, we used the NOW database in our analysis. An attempt was made to supplement our dataset using the Paleobiology Database (PBDB, http://paleodb.org) using the NOW taxonomy system as the basis, given the abundance of taxonomic inconsistencies and outdated information in PBDB (Prothero 2015). However, we abandoned the effort due to the difficulty of avoiding a large number of duplicate entries due to synonyms, and differences in taxonomic classification even at the order level. In addition to that, PBDB contains a large number of entries dated at around the Paleocene–Eocene thermal maximum (PETM), for instance, a large sample described in (Clyde 1997), which would have introduced a source of significant bias.
A comparison of temporal distribution between Artiodactyla, Carnivora, and Perissodactyla occurrences in NOW and PBDB is shown in Fig. A1A. In both datasets, the number of occurrences sharply decreases pre-Miocene, with PBDB having relatively more records in Oligocene, Eocene, and Paleocene. However, PBDB has significantly fewer records from Miocene and later epochs than NOW.
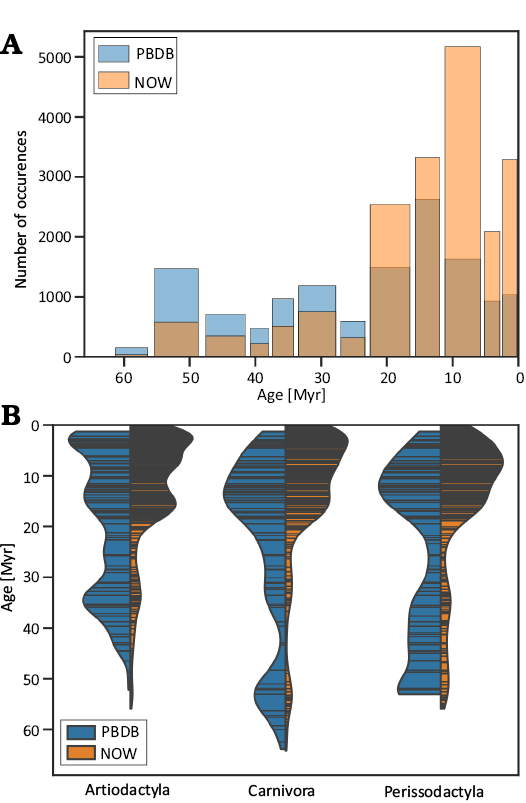
Fig. A1. A. Age distribution of NOW and PBDB Artiodactyla, Carnivora, and Perissodactyla occurrences. B. Temporal distribution of NOW and PBDB Artiodactyla, Carnivora, and Perissodactyla locality ages and relative abundances of localities, represented on the x-axis. Violin plot widths are scaled and do not reflect relative locality abundance distributions between different orders.
An additional problem with the PBDB data is different age resolution and sampling frequency, shown in Fig. A1B. For the three orders under consideration, the average interval between maximum and minimum occurrence ages is 1.47 Myr for NOW and 3.97 Myr for PBDB. In the two datasets, there were 642 unique age intervals (i.e., combinations of maximum and minimum ages) in NOW and only 105 in PBDB. Although including PBDB occurrences, especially from before Miocene, would have improved the temporal and spatial coverage of our sample, manually curating a combined sample was not feasible.
Geographical distribution of the NOW localities is shown in Fig. A2, showing that the majority of taxa lived in temperate latitudes of Europe, Eastern Asia and Western North America. A distinct feature is a concentration of older (~55 Myr) localities in Western North America, most likely owing to large research interest in PETM. African localities are mostly limited to North and East Africa. Global extinction and origination processes are spatially heterogeneous (Flannery-Sutherland et al. 2022), and new methods that account for spatial biases in paleontological data are emerging (Flannery-Sutherland et al. 2022; Antell et al. 2023). We defer spatial coverage analysis to subsequent work, assuming that the global changes in diversity trajectories will be reflected in our dataset, and that the main source of bias in it is instead the uneveness in temporal sampling, as discussed below.
Temporal distribution of localities, families, genera, and species for all orders together and separately is shown in Fig. A3. Given the nature and history of the NOW database (Fortelius et al. 2023) and the fossil record in general, we cannot assume that our dataset is homogeneous, representative or complete throughout the Cenozoic. Instead, we aim to evaluate the adequacy of the fossil record for the task on hand (Benton et al. 2011).
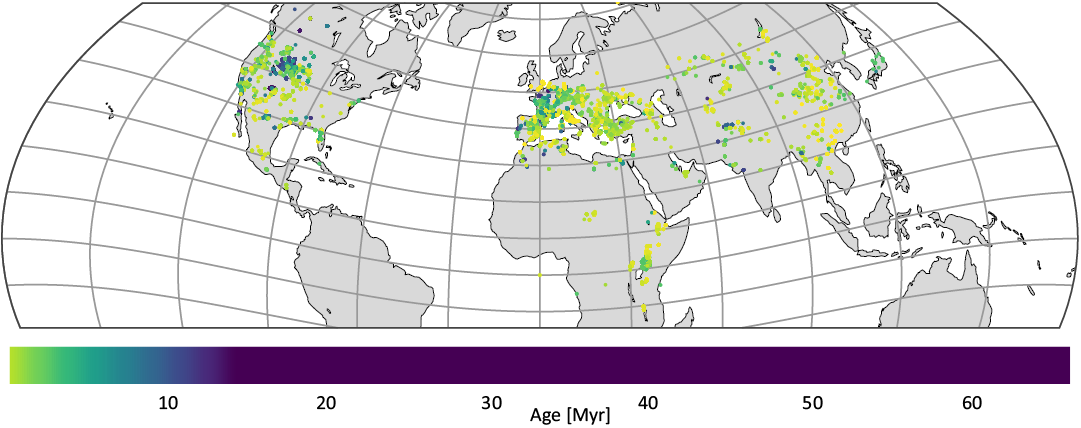
Fig. A2. Geographical distribution of Artiodactyla, Carnivora, and Perissodactyla occurrences in our NOW sample.
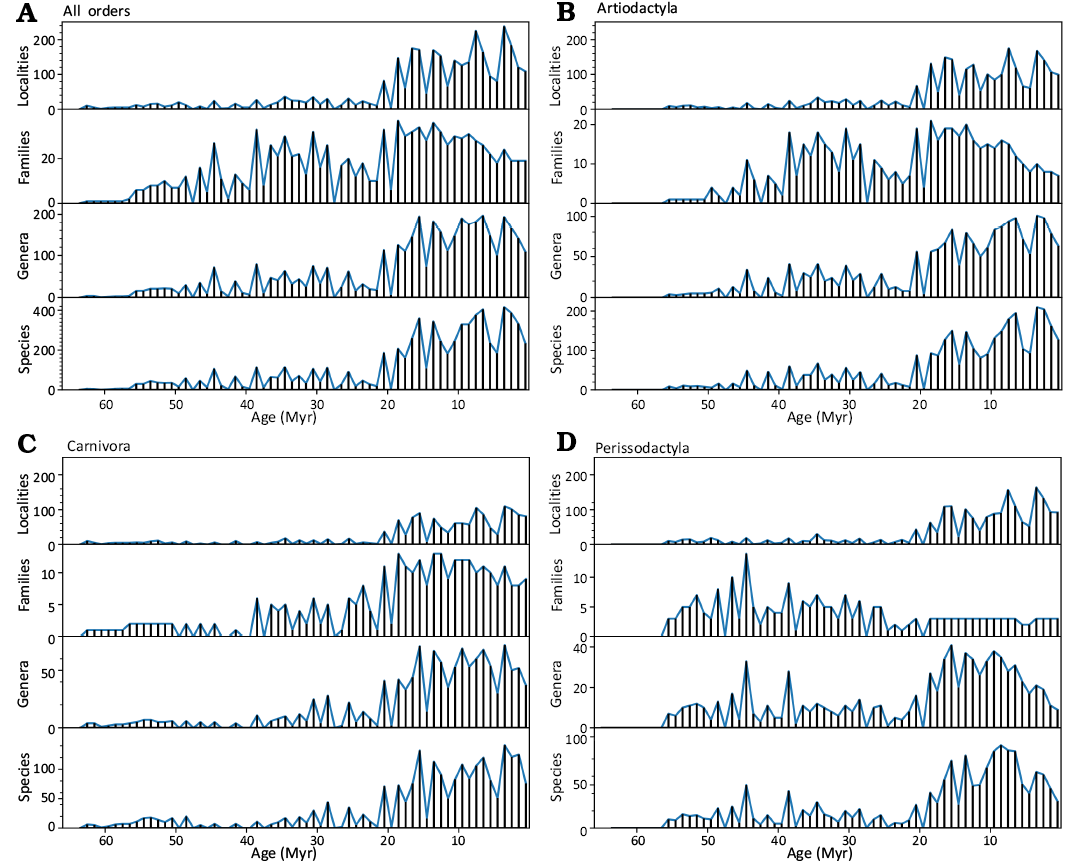
Fig. A3. Locality count, family, genera, and species number distributions in 1 Myr bins for all three orders (A), Artiodactyla (B), Carnivora (C), and Perissodactyla (D).
A clear drop of locality counts is visible at approximately 21 Myr, matching a similar drop of species and genera occurrence counts. At taxonomic level of families, the fossil record is expected to be more homogeneous and reflect the broad patterns of diversification more robustly (Benton et al. 2000). Indeed, family occurrence counts do not co-vary with locality or species and genera counts for Artiodactyla and Perissodactyla. In the latter case, the decrease of families since the beginning of Miocene, even though localities, species and genera counts are increasing, illustrates the dramatic loss of higher taxonomic level Perissodactyla diversity. Correspondence between Carnivora family, genera and species count patterns is closer than for the other two taxa, suggesting that the species and genera-level data reflects the overall Carnivora diversification pattern.
A quality measure of the fossil record over time is the ratio of occurrences of recognised species (main sample) and of all occurrences including undefined species (control sample), a generalisation of specimen-level fossil quality measures described in literature (Mannion and Upchurch 2010; Benton et al. 2011). To obtain the control sample from the NOW database, we repeated the sample selection steps described in the Material and methods section, retaining all occurrence records where the species name was missing (i.e., it was marked as “indet.”, “sp.” or was an empty string). This sample contained 12 017 Artiodactyla, 6825 Carnivora and 6040 Perissodactyla occurrences resolved to a genus or species level. A comparison with our main species-resolved sample (9081 Artiodactyla, 5379 Carnivora, and 4766 Perissodactyla occurrences) shows that 76% of Artiodactyla, 79% of Carnivora, and 79% of Perissodactyla occurrences in our main sample were resolved to a species level. On average, each Artiodactyla species were represented by 5.4 occurrences, Carnivora, 4.9 occurrences, Perissodactyla, 6.5 occurrences in the main sample. The temporal evolution of the ratio of occurrences defined to the species level over the control sample occurrence counts is shown in Fig. A4A. Although the ratio is relatively uniform, several gaps are visible, especially between ~38–48 Myr for Carnivora, at ~48 Myr for the remaining orders, and at ~28 Myr for all orders.
As described in the Material and methods section, the PyRate framework (Silvestro et al. 2014, 2019), which we use for diversification analysis, provides absolute preservation rate estimates over time, i.e., the average number of expected occurrences of fossils per species per Myr. We show preservation rates together with estimates of the sampling quality in Fig. A4. Interestingly, Carnivora preservation rate estimates throughout Aquitanian–Chattian (20.44–27.82 Myr) are much lower for Carnivora compared to the other two orders. A significant sampling probability decrease for Carnivora pre-Miocene is also reported in literature (Liow and Finarelli 2014). Conversely, Carnivora preservation rates in Eocene and Paleocene are higher than those of the herbivore orders.
Relative variation of fossil preservation sampling quality over time was estimated for species and genera in 2 Myr intervals using functionality provided by the divDyn R package (Kocsis et al. 2019). The three-timers sampling rate estimate (Alroy 2008) throughout the study period is defined in a moving window of three time bins as the ratio of the number of taxa present in the focal interval and also in the preceeding and the following intervals (three-timers, 3t), and the sum of three-timers and the number of taxa found in the preceding and the following intervals, but not detected in the focal interval (part-timers, Pt). We also estimated Good’s u coverage estimator (Good 1953) using divDyn.
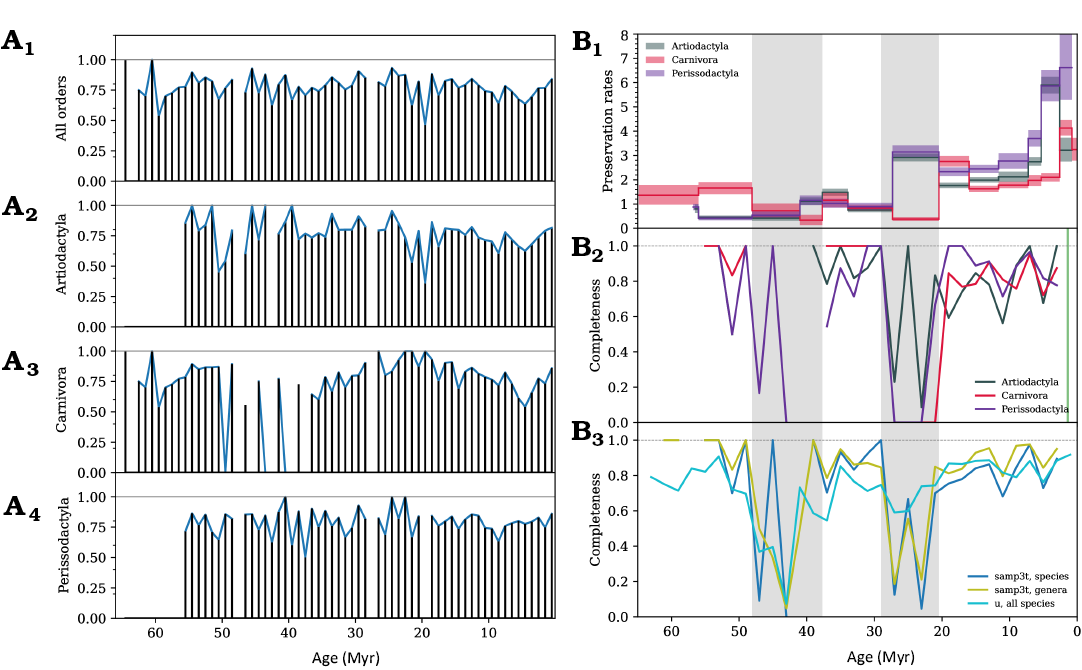
Fig. A4. A. Well-defined species fraction through time in 1 Myr bins for all three orders together (A1) and separately (A2–A4). B. Various measures of sampling quality through time. B1, PyRate preservation rates for the three clades; B2, three-timer sampling completeness for Artiodactyla, Carnivora, and Perissodactyla species; B3, comparison of three-timer sampling completeness at species and genera level, and Good’s u measure for species in all three orders. Grey shading marks the intervals of inadequate fossil record quality.
We find that the three-timers sampling estimate, which uses the proportion of gaps in the taxa occurrence record, is not always applicable due to the fact that the average duration of large mammal species and genera is estimated to be 2.17 Myr and 3.94 respectively (Liow et al. 2008), and thus just a small fraction of all taxa can be detected in three consecutive time intervals. In some intervals this leads to the species-level completeness estimates being undefined, as shown in Fig. A4B. For the whole sample (bottom right panel), species-based, genera-based and Good’s u estimates agree well.
Although PyRate’s preservation rate estimates and sampling completeness estimates shown in Fig. A4 correspond to different properties of the sample, common patterns can be inferred. There are indications of two significant dips in sampling coverage in Oligocene and Eocene, although the severity of sampling quality decrease differs between different clades. For instance, Artiodactyla may not be so badly affected through the Oligocene as the other two orders, as suggested by both PyRate preservation rates and three-timer and u sampling estimates. A similar fossil record completeness pattern for ruminants, with a significant decrease in Oligocene and the first half of the Eocene is also reported in (Cantalapiedra et al. 2015).
Irrespective of whether the reasons of fossil record quality decrease between approximately 20–29 Myr and 38–48 Myr stem from low abundance and diversity, idiosyncrasies of the NOW database or from heterogeneities in geological completeness of paleontological sampling (Peters and Heim 2010), species diversity and diversification measures such as speciation and extinction rates should be treated with caution during these intervals. We mark them with gray shading throughout the analysis.
Centrality of recurrence
The centrality of recurrence measure (CEN, Spiridonov et al. 2017) estimates the time uniqueness of a system’s state at specific times. The time uniqueness or time-anomality, a geobiological phenomenon having a long history in research (Jeppsson 1987; Brett and Baird 1997) can appear in several ways. For example, it can be a result of a strong trend which generates non-repeating states, or it a result of the intercalation of non-trending time-specific states which exhibit unique (non-repeating at other times) characteristics.
The CEN metric can comprehensively describe different kinds of dynamics. In our case, if diversity reaches very similar values or dynamical patterns at the opposite sides of the time series, then we would expect very low values of CEN since dispersion is penalised. The internal variability of dynamic states (expressed as a low recurrence rate) is also penalised and would yield low values of CEN.
Time-specific states in recurrence plots of paleontological time series appear as squares or square-like structures saturated with black (recurring) points. Even if two states could be completely separate and distinct in the larger context, they still would differ in their internal variability and dynamic cohesion. If, for example, a state is highly distinct from other states and varies little in time during a time period, this state will appear as a highly saturated square in a recurrence plot – it will have a high density of points. In this case, the state will have high CEN values. On the other hand, if the state is highly distinct from other time periods, but there is high variability within the state, then this state will show low time uniqueness (i.e., low CEN values).
The CEN measure can be applied to univariate as well as to multivariate time series auto-recurrence plots, as well as the joint recurrence plots applied here in order to investigate the common correlational structures in qualitatively different systems. CEN series of the three diversity—δ18O joint recurrence plots and of the triple JRP of Artiodactyla, Carnivora, and Perissodactyla are shown in Fig. B1. As explained before, the peaks in CEN series denote intervals which are coherent and time-unique in terms of δ18O and species diversity.
The first time-specific climate-diversity state corresponds to the Ypresian stage of the Eocene Hothouse. The second and the third peaks correspond to the Lutetian and to Bartonian–Priabonian stages of the Eocene, during the second stage of Cenozoic Warmhouse (Westerhold et al. 2020). The fourth peak corresponds to the Oligocene epoch and the beginning of the Coolhouse climatic regime. A subsequent decrease in CEN approximately corresponds to most of the Miocene epoch (up to 10 Myrs BP). Finally, the Quaternary period corresponds to the fifth peak of climate-diversity CEN. It is caused by a coherent and persistent drop in temperatures through this period and also by the persistent drop in diversity of all three clades.
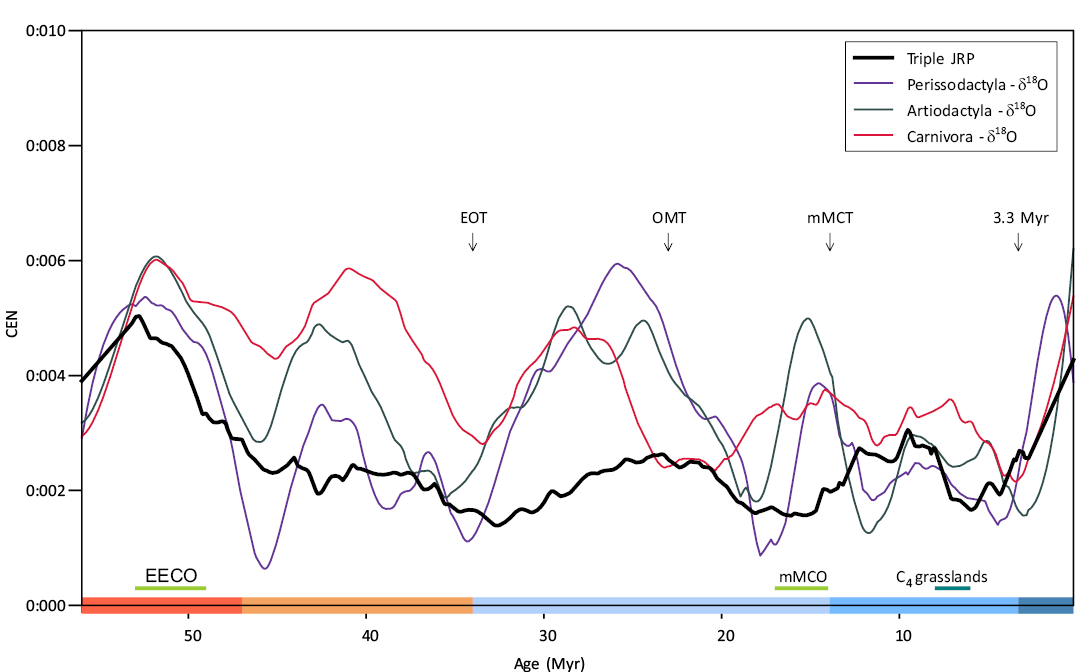
Fig. B1. CEN series of the three joint recurrence plots and of the triple joint recurrence plot (JRP) of Artiodactyla, Carnivora, and Perissodactyla. Coloured ranges indicate the Earth climate states (Hothouse, Warmhouse, two Coldhouse states, and Icehouse) (Westerhold et al. 2020). Abbreviations: C4 grasslands, onset of C4 grassland spread, 3.3 Myr: onset of the Icehouse regime 3.3 Myr ago; EECO, Early Eocene Climatic Optimum, EOT, Eocene–Oligocene Transition; mMCO: middle Miocene Climatic Optimum; mMCT, middle Miocene Climatic Transition; OMT, Oligocene–Miocene Transition.
The triple-JRP CEN, utilising no climate data, shows two exceptional states of diversity dynamics, during the Eocene and Quaternary, indicating that the dramatic diversity decrease is non-precedented in the evolutionary history of the clades. It could be stipulated that the diversity drop can be explained by stronger Coolhouse and Icehouse climate forcing by long-period Milanković cycles and by their impact on the diversification process, detected in the Neogene (Van Dam et al. 2006) as well as in end-Ordovician and Silurian cold climate states (Crampton et al. 2016, 2018). In each time step, there is a monotonous drop in diversity, and due to this monotonicity, the neighbouring diversity states are very similar and not co-recurring in all three clades at the same time with the states at other times. This gives credibility to the supposition that the Quaternary is an objectively distinct state of Earth’s climate and biodiversity, and not a part of the Neogene, as was suggested in some earlier stratigraphic works (see Lourens 2008).
Conceptual explanation of the macroevolutionary conclusions
We present a conceptual illustration (Fig. C1) of the comparison between the dynamic coupling of diversity-climate co-evolution and the classical picture of macroevolutionary response to environmental change (Alroy 2010). Both paradigms predict significant transitions between diversity regimes after climatic changes, however, we demonstrate that the resulting diversity regimes are not autonomous states independent from the driving climate. Diversity trajectories are coordinated with the multistable states of the megaclimate, the evolution of which drives sharp transitions to alternative diversity levels.
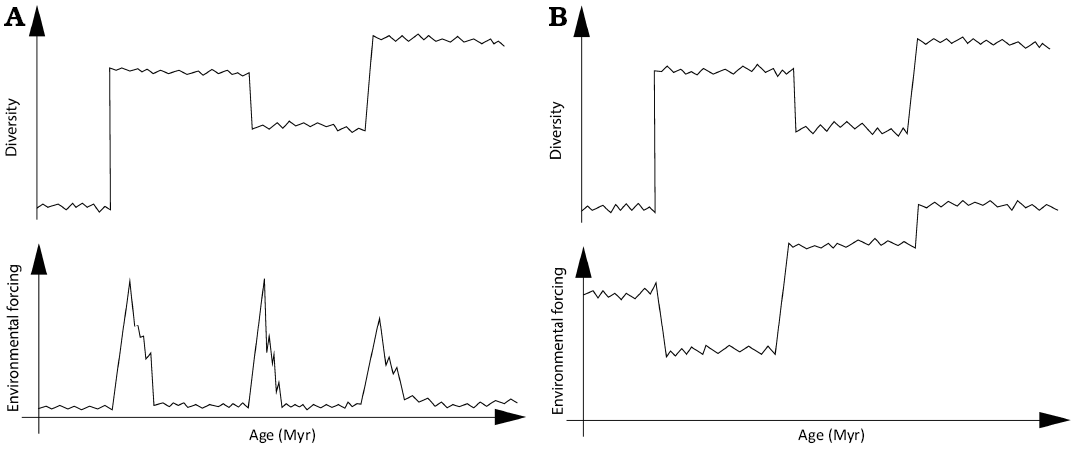
Fig. C1. A conceptual drawing of the comparison of our conclusions and the shifting balance of clades hypothesis. A. The shifting balance hypothesis predicts that extreme global perturbations randomise the carrying capacities and other diversification parameters of higher clades. B. The pattern revealed in this study for large-bodied Cenozoic mammals. Illustration by Gerda Vaitkevičiūtė.
Acta Palaeontol. Pol. 70 (3): 479–494, 2025
https://doi.org/10.4202/app.01145.2024